Formulaire de l'Analyse en Composantes Principales
(J.Ph. Labat)

 Matrice des données : m objets (ou individus), p descripteurs (ou variables) :

 Centrage et réduction des données :

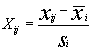
 Distances entre objets:

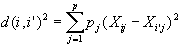
ou pj est une pondération qui est en général égale à 1.

Inertie totale I du nuage est égale à

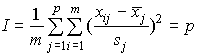
Réalisation de l'analyse en composantes principales :

Le but : trouver des axes orthogonaux (indépendants) qui ont la propriété d'extraire le maximum de la variance projetée (ou inertie projetée) des individus ou objets. 

• calcul de la matrice des données centrées-réduites.
• calcul de la matrice des corrélations variables/variables.
• calcul de la matrice des vecteurs propres et du vecteur des valeurs propres. (rappel de calcul matriciel)
  

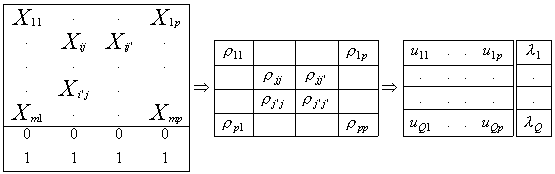
Avec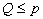

• Les vecteurs propres sont les coordonnées du point de norme 1 des nouveaux axes sur les anciennes variables. Les valeurs sont proportionnelles à la variance associée à ces axes.
• Calcul des cordonnées des individus sur les nouveaux axes.
• Calcul des corrélations des variables avec les nouveaux axes.
  

Relations de transitions

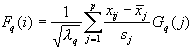
ou F est la projection de l'individu i sur l'axe factoriel q, G les projections des p variables sur q, et l la valeur propre associée à la composante q.

et par réciprocité:

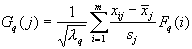
 Nuage des variables:

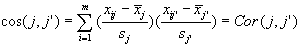
J. Ph. Labat, Mise à jour : 18/11/04